
This physical representation makes calculations easy and allows the viewer the visualize angles that do not make sense when only considering the triangle itself, such as obtuse angles and reflex angles. The sine and cosine then are just the lengths of the vertical segment and the horizontal segment respectively. In this triangle, the hypotenuse is a radius of the circle, so it has a length of $1$. A vertical line segment connecting the intersection of the terminal radius and the circumference to the x-axis creates such a triangle. Then, it is simple to create a right triangle using these radii. These angles are easily denoted by the point at which their terminal angle intersects the circumference of the circle. The unit circle is incredibly important in trigonometry because it is easy to create angles using the radii of this circle. It lies in the Cartesian coordinate plane with a center at the origin, $(0, 0)$. While the unit circle is fundamental to trigonometry, it is also important in all branches of science, mathematics, and engineering that use trigonometry.īefore we move on with the information of this section, make sure to review trigonometric ratios and angles.Ī unit circle has a radius of one unit.
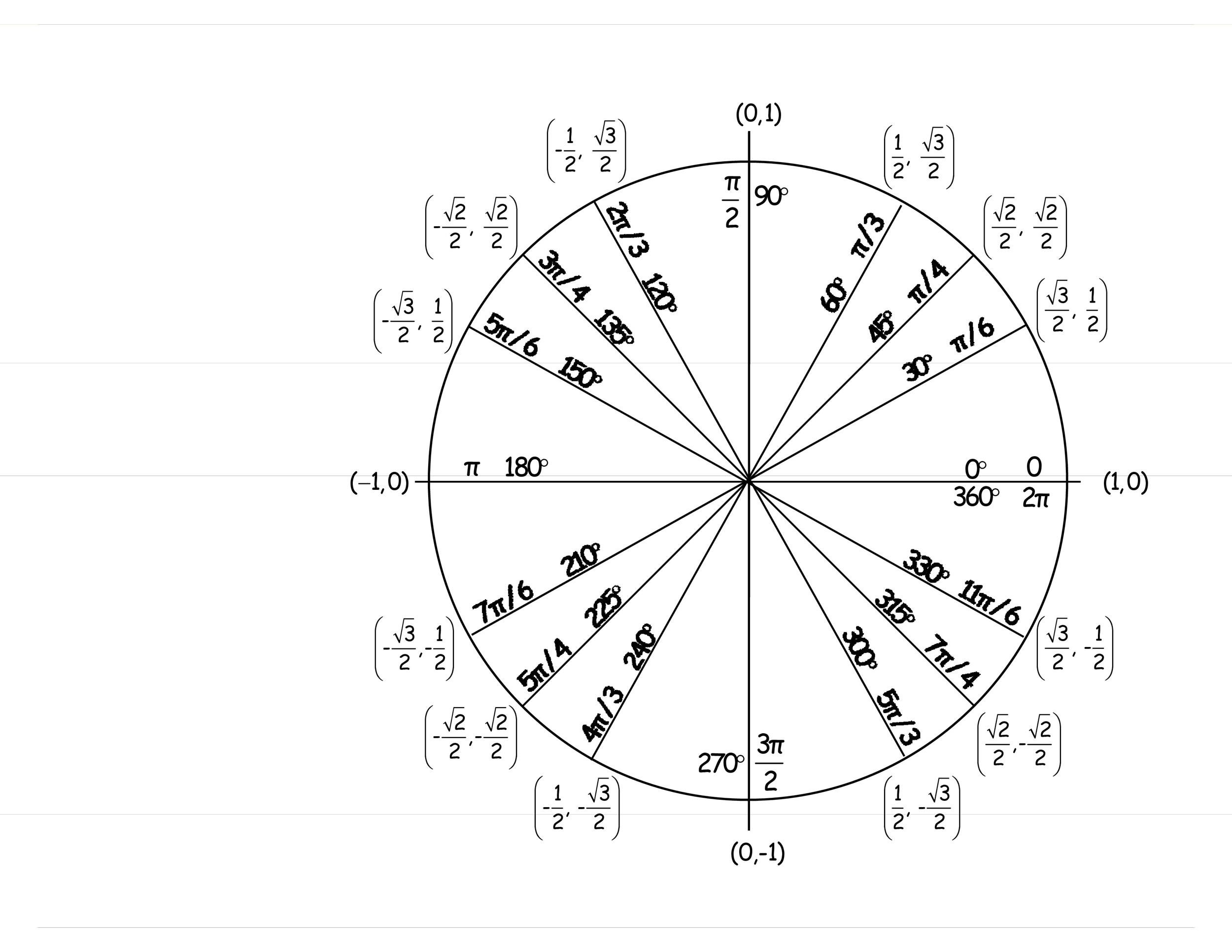
Then, the orientation in the plane helps determine positive and negative values for trig functions.

Typically, the initial angle is the line segment extending from the origin to the point $(1, 0)$. This circle is useful for analyzing angles and trigonometric ratios.
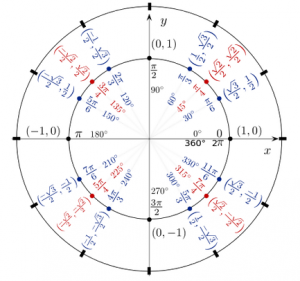
The unit circle is a circle in the Cartesian plane centered at the origin and with a radius of $1$.


 0 kommentar(er)
0 kommentar(er)
